社会で一番多く使われているのが三角関数ですよね。移動距離を求めたり、ゲームなんかにも多用されています。まぁ辺の長さを計算する場合は電卓ですけどね。このサイトでは、公式を覚えることよりなぜそうなるのか、どうしてなのか思考することを意識します。CADの解析で必要な思考力をみにつけることが目標ですのでご了承ください。
三角関数の定義
重さの単位と同じように決まり事なので、この見出しではとくに解説はありません。
定義
三角関数に触れてない方はこの際に覚えておきましょう。
覚えなくても、使っているうちに覚えちゃうかもね。直角三角形の比率を表します。それだけ…
$$\frac{y}{z}=\sin\theta{ ⇒}\frac{対辺y}{斜辺z}$$
$$\frac{x}{z}=\cos\theta{ ⇒}\frac{底辺}{斜辺}$$
$$\frac{x}{y}=\tan\theta{ ⇒}\frac{底辺}{対辺}$$
基本公式は覚えない主義ですが、上記は決まり事なので覚えてください。
使い方
CAD 解析サイトなので三角関数の使い方はとても重要です。
sin、 cos、tanは直角三角形の辺の比率をあらわしているだけなので、角度と1辺の長さがわかれば他の部分は全て算出できます。角度θが30°斜辺zが10の場合yは
$$y=10\sin30=5$$
角度θが30°斜辺zが10の場合xは
$$x=10\cos30≒8.6$$
$${角度θが30°底辺は}10\cos30{ その場合yは}$$
$$y={10\cos(30)}{\tan(30)}=5$$
計算は電卓かエクセルでやってね。
注意：コンピューターはプログラミング上ラジアンで計算していますので、エクセルの場合はラジアンで入力してください。COS(RADIANS(30))みたいな…
最大値と最小値
三角関数には最大値と最小値が存在します。
円による三角関数 sin
円の中に直角三角形を描くと三角関数の最大値と最小値がわかります。動画と組み合わせてかんがえてもらうとわかりやすいですよ。円の画像を見ながら想像してね。
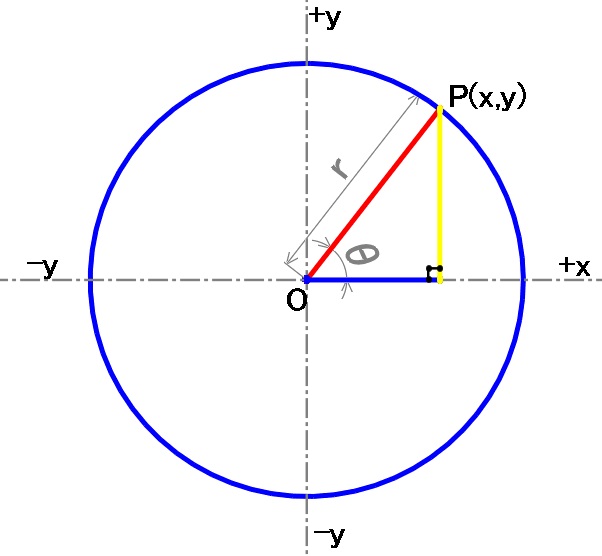
$$r\sin0=r\times0=0$$
θが45°の場合黄色線の長さxは
$$x=r\sin45{≒}0.7r$$
θが90°の場合黄色線の長さxは
$$x=r\sin90=1\times{r}=r$$
円による三角関数 cos
角度θが0の場合の青色線の長さは
$$r\cos0=r\times1=r$$
角度θが45°の場合、青色線の長さは
$$r\cos45{≒}0.7r$$
θが90°の場合の青色線の長さは
$$r\cos90=r\times0=0$$
円による三角関数 tan
タンジェントは少し変
θが0の時の黄色線の長さは
$$r\tan0=r\times0=0$$
θが45の時、黄色線の長さは
$$r\tan0=r\times1=r$$
θが90の時は円の画像で想像すると
$$r\tan90=r\times?=?$$
tan90は1÷0になります。これって割り算できませんよね。tan90はありません。タンジェントだけは変な関数です。
今回は三角関数公式と最大値最小値を円を使って考察しました。設計道具のCAD CAEを使うにしても必ず登場する関数です。どんな仕組みになっているのかイメージできれば大成功です。だって計算は電卓やCADで簡単にできちゃうので。
今回使った円画像は次回も利用します。三角関数はただの直角三角形の辺の比率であることをイメージしたいと思います。
長くなりましたが、このページはこれでおしまいです。
お疲れさまでした。
コメント