前回に引き続き三角関数の最大値最小値ですが、角度によってはマイナスの値もあります。CAD CAE解析ではあまり出番がありませんが、周期のグラフを作る際には重要な要素になります。特にSimulationXpressは自分で力の要素を考察する必要があります、その際には間接的に必須科目です。
三角関数は直角三角形の辺の比率
三角関数なんてカッコいい言葉ですが、ただの辺の比率でしかありません。
半径 = 1の円で考える
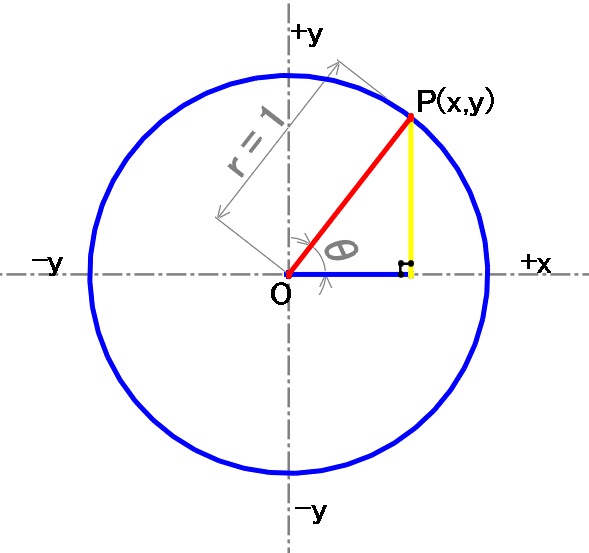
三角関数表を見るとsin、cos、tanは全て角度だけできまります。半径のrは1にしても比率の変更がありません、つまり三角関数はr=1でも同じ値が得られるということです。
よく物理や数学の教科書にr=1で説明されているのはそのためです。
各三角関数とりうる値の範囲
sin、cos、tanは円の領域のPの位置で値が変化しますが、範囲があります。
「sinθ」の場合

画像では
$$\sin{30}=\frac{x}{y}=\frac{0.5}{1}=0.5$$
になります。
P点が黄色の領域ではsinの値はマイナスです。
$$-1{ ≦ }\sin\theta{ ≦ }1$$
「casθ」の場合

$${ヒント }0.9{ ≒ }\frac{\sqrt{3}}{2}$$
以下の意味もちゃんと考えてね。
$$\frac{\sqrt{3}}{2}$$
当サイトの目的が理解イメージすることなのでこんな問題になってます。
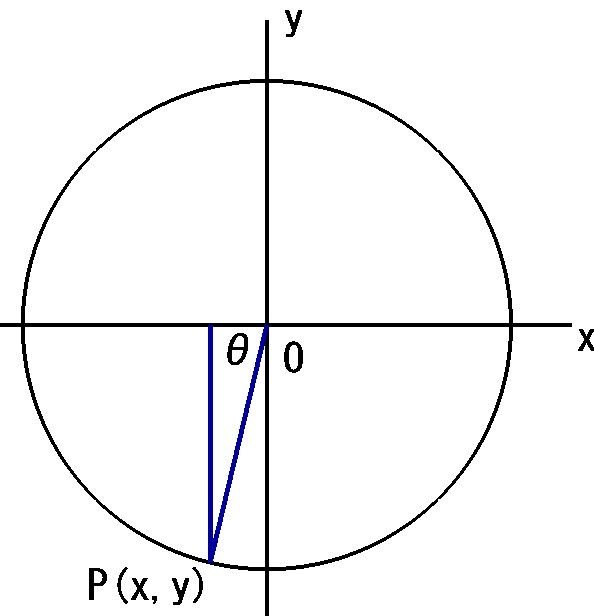
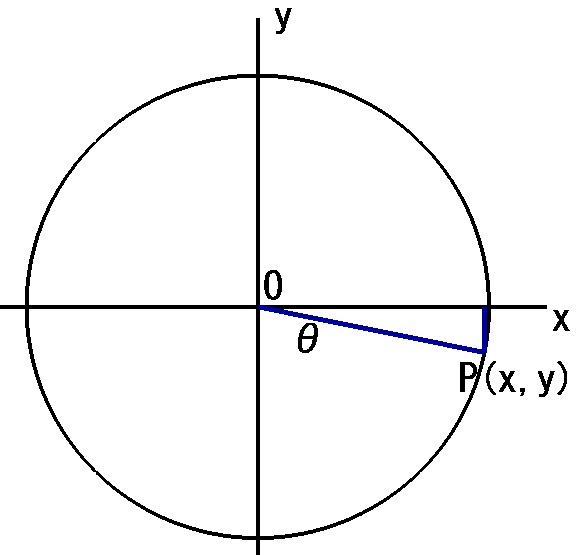
「tanθ」の場合
いろいろな角度に対するtanθを求めると、取りうる値がわかってきます。下の画像はわかりやすいようにP点をなるべくx軸y軸に近づけてみました。
この場合も質問形式です。
「tanθ」の値の範囲はどこからどこまででしょうか。
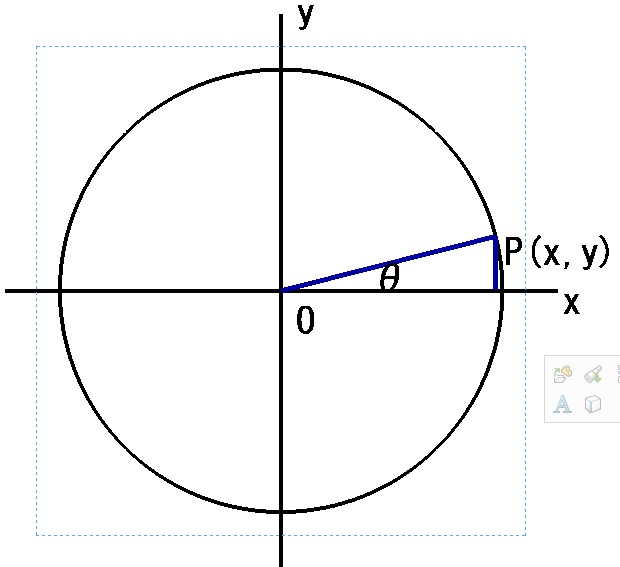 |  | 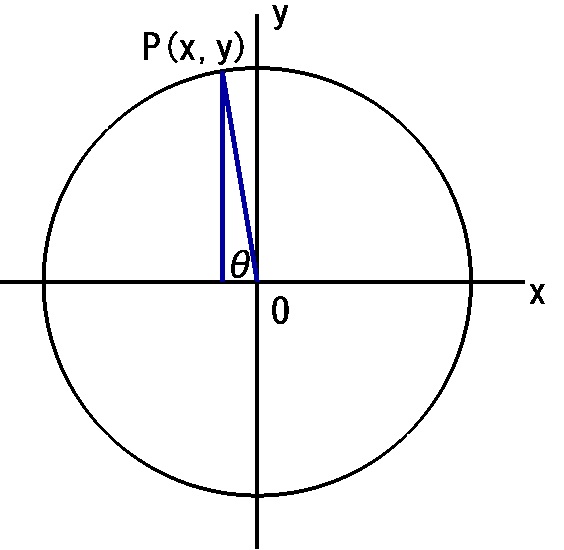 |
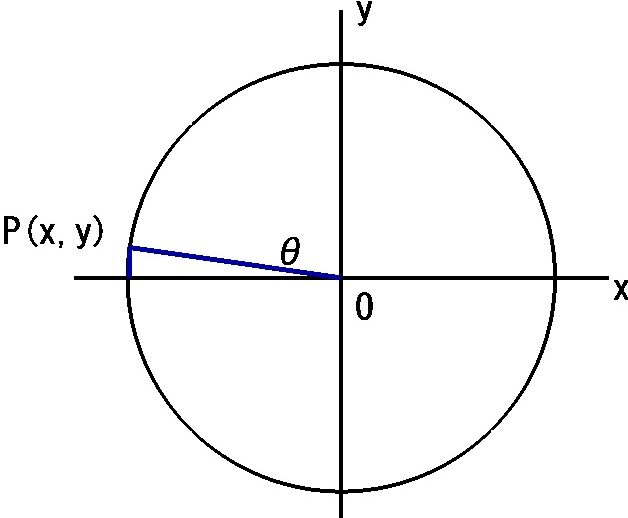 |  |  |
 | ヒント;人間には想像がつかない値もある。 電卓だと計算できなことも
| |
答えはイメージできればおっけーです。覚える必要はありません、使ってるうちにおぼえちゃいますので…
前回に引き続き三角関数の取りうる値についての解説、今回は負の値があることに特化しました。
負の値があることにより、有名なsinカーブ、cosカーブが存在できることになります。くわしいいことは次のページに掲載します。
このページはこれでおしまいです。
お疲れさまでした。

コメント