sinθ、cosθ、tanθには三角関数の相互関係っていうものがあります。感の良い方はすぐ思いついたと思います。CADの設計しかも3Dだから自分には関係がありませんと思っているかもしれませんが、解析の場合は時々必要なことがあります。特にSimulationを利用する場合は知っていて損がありません。毎回ですが公式を丸暗記することは推奨しません。
三角関数の相互関係公式
三角関数の相互関係の公式一覧
$$\cos^2\theta+\sin^2\theta=1$$
$$\tan \theta=\displaystyle \frac{\sin \theta}{\cos \theta}$$
$$\tan^2 \theta+1=\displaystyle \frac{1}{\cos^2 \theta}$$
当サイトは設計者が解析するための技術をみにつけるサイトですので、公式を覚えるのではなく、どうしてその公式が成り立っているのか、どうしてそうなるのかを考察します。ご了承ください。
cos²θ+sin²θ=1
上記の式は感のいい方ならもうわかっちゃいますよね。そうあれですよ。
図を見ると一目瞭然
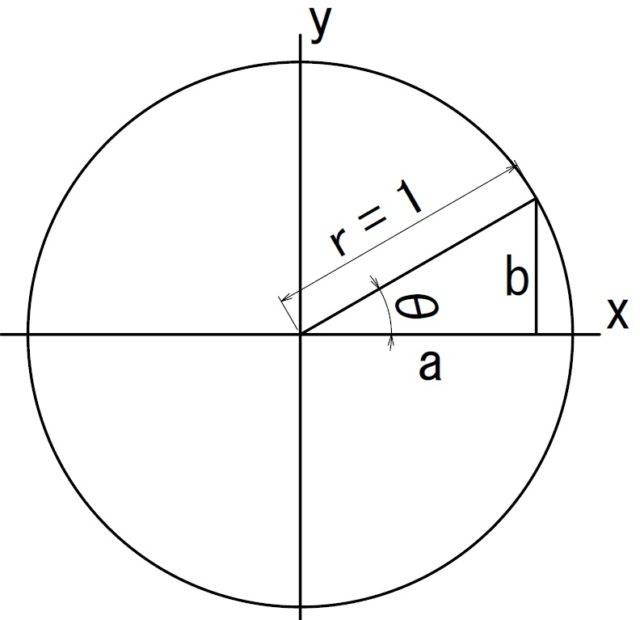
$$r^2=a^2+b^2$$
式に値を代入します。
$$a=r*\cos\theta$$
$$b=r*\sin\theta$$
$$r^2=r*\cos^2\theta+\sin^2\theta$$
三角関数はただの直角三角形の辺の比率なので、r=1にしてもおっけー。
$$\cos^2\theta+\sin^2\theta=1{となります。}$$
tanθ=sinθ/cosθ
この公式は上図に辺の値を代入するだけ。
この式はイメージなしでおっけー
$$\tan\theta=\frac{b}{a}$$
$$\tan\theta=\frac{r*\cos\theta}{r*\sin\theta}$$
$$\tan\theta=\frac{\cos\theta}{\sin\theta}$$
以上で完了です。かんたん
tan²θ+1=1/cos²θ
この公式もCAD設計の解析ではときどき使います。公式といっても上図に値を代入するだけです。
値の代入
$$\tan\theta{の値 }\tan\theta=\frac{b}{a}$$
$$\tan^2\theta=\left( \frac{b}{a} \right)^2$$
$$\cos^2\theta=\left( \frac{r}{a} \right)^2$$
三平方の定理より以下の式が成立します。
$$a^2+b^2=r^2$$
式に値を代入すると
$$\cos^2\theta+b^2=r^2$$
$$1+\frac{b^2}{cos^2\theta}=\frac{r^2}{\cos^2\theta}$$
$$1+\left( \frac{b}{a} \right)^2=\left( \frac{r}{\cos\theta} \right)^2$$
$$\tan^2\theta+1=\frac{r}{\cos^2\theta}$$
三角関数は単なる辺の比率なのでr=1でもよい
$$\tan^2\theta+1=\frac{1}{\cos^2\theta}$$
式に値を代入するだけの公式です。
今回のテーマは三角関数の相互関係の公式の解説でした。式に値を代入するだけのものであまりイメージする場面がありませんでしたが、三平方の定理のように面積を利用して値を代入して式をみちびきだすこともありますので、まんざらでもないないですよね。
公式は覚える必要はありません。よく使う場合は自然と覚えちゃいますので…
このページはこれで終了です。
お疲れさまでした。
